With summer here, I've had some time to square away some projects I've been working on. It's been great to reconnect with them after all the craziness that comes with the end of the semester. I'll devote a post to each of the projects I've been working on over the last little while.
Denise Troxell, Sarah Adams and I advise a group of Olin undergraduates who work on discrete problems, usually centered on $L(d,1)$-labelings of graphs. This research stems from the frequency assignment problem in wireless communications: how do you assign frequency bands to spatially distributed transmitters such that transmitters that are in close proximity to one another use frequencies that are sufficiently spectrally separated to avoid interference?
Mathematically, we consider the transmitters to be the vertices of a graph $G$, with vertices $x$ and $y$ adjacent if the associated transmitters are closer than some distance threshold. We can then think of a "good'' frequency assignment as a function $f : V(G) \rightarrow \{0,1,2,...,c\}$ such that $|f(x) - f(y)| \geq d$ if $x$ and $y$ are adjacent and $|f(x) - f(y)| \geq 1$ if $x$ and $y$ are at distance 2 in $G$. This is an $L(d,1)$-labeling of $G$. For a fixed graph $G$, the minimum value of $c$ over all $L(d,1)$-labelings is denoted $\lambda_d(G)$. A lot of work has been dedicated to determining $\lambda_d(G)$. The major open conjecture in the field was made by Griggs and Yeh and states that $\lambda_2(G) \leq \Delta^2$, where $\Delta$ is the maximum degree of $G$. Georges, Mauro, and Whittlesey show that determining $\lambda_d(G)$ is NP-Complete in general. This has motivated many researchers, including those in our group, to investigate classes of graphs that are of practical or theoretical interest.
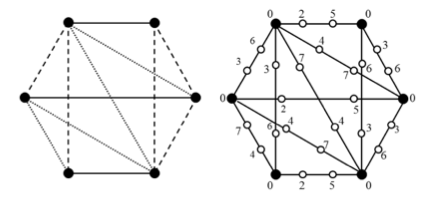
Our newest piece of work, just accepted to the Journal of Combinatorial Optimization, deals with so-called edge-path replacement graphs. Here we replace each edge of a graph $G$ with a path $P_k$ on $k$ vertices to form $G(P_k)$. This is a really interesting problem, because degree and distance play such large roles in $L(d,1)$-labelings. By adding these paths, we're in some sense increasing the distance between high degree vertices while at the same time preserving the maximum degree of the graph.
Denise Troxell, Sarah Adams and I advise a group of Olin undergraduates who work on discrete problems, usually centered on $L(d,1)$-labelings of graphs. This research stems from the frequency assignment problem in wireless communications: how do you assign frequency bands to spatially distributed transmitters such that transmitters that are in close proximity to one another use frequencies that are sufficiently spectrally separated to avoid interference?
Mathematically, we consider the transmitters to be the vertices of a graph $G$, with vertices $x$ and $y$ adjacent if the associated transmitters are closer than some distance threshold. We can then think of a "good'' frequency assignment as a function $f : V(G) \rightarrow \{0,1,2,...,c\}$ such that $|f(x) - f(y)| \geq d$ if $x$ and $y$ are adjacent and $|f(x) - f(y)| \geq 1$ if $x$ and $y$ are at distance 2 in $G$. This is an $L(d,1)$-labeling of $G$. For a fixed graph $G$, the minimum value of $c$ over all $L(d,1)$-labelings is denoted $\lambda_d(G)$. A lot of work has been dedicated to determining $\lambda_d(G)$. The major open conjecture in the field was made by Griggs and Yeh and states that $\lambda_2(G) \leq \Delta^2$, where $\Delta$ is the maximum degree of $G$. Georges, Mauro, and Whittlesey show that determining $\lambda_d(G)$ is NP-Complete in general. This has motivated many researchers, including those in our group, to investigate classes of graphs that are of practical or theoretical interest.
Our newest piece of work, just accepted to the Journal of Combinatorial Optimization, deals with so-called edge-path replacement graphs. Here we replace each edge of a graph $G$ with a path $P_k$ on $k$ vertices to form $G(P_k)$. This is a really interesting problem, because degree and distance play such large roles in $L(d,1)$-labelings. By adding these paths, we're in some sense increasing the distance between high degree vertices while at the same time preserving the maximum degree of the graph.
Our solution to this problem involved decomposing $G$ using a 2-factorization, and then labeling each of the 2-factor separately using a specific scheme. The results prove a conjecture made by Lu: for any graph $G$ with $\Delta \geq 2$, $\lambda_2(G(P_4)) \leq \Delta + 2$. Ours are significantly more general: for any graph $G$ with $\Delta > 2$, $\lambda_d(G(P_k)) \leq d + \lceil \Delta /2 \rceil + \max ( \lceil \Delta / 2 \rceil, d) $ for any $d \geq 2$ and $k \geq 4$. The case with $\Delta \leq 2$ deals with graphs that are unions of paths and cycles, and the $L(d,1)$-labelings of these graphs are well understood. The case of $k = 3$ is the so-called total labeling of $G$ and is significantly harder. In some cases we can do a little bit better than the bounds I've quoted here.
All in all, the project was a great team effort. It's great to work with such bright and motivated undergrads. It looks like both Jessica and Jason are going to stick around next semester, so look for more great work to come from these two.
All in all, the project was a great team effort. It's great to work with such bright and motivated undergrads. It looks like both Jessica and Jason are going to stick around next semester, so look for more great work to come from these two.
 RSS Feed
RSS Feed
